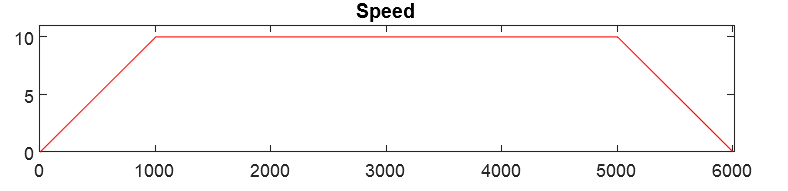
Move Physics: Trapezoidal speed profiles
1. Kinematic Quantities
Let’s define instantaneous: An instant value of time t.
From the instantaneous position \(x = x(t)\), the instantaneous velocity \(v = v(t)\) and acceleration \(a = a(t)\) have the general and coordinate independent definitions as following:
\(v = \frac{dx}{dt}\) and \(v = \frac{dv}{dt} = \frac{d}{dt} \frac{dx}{dt} = \frac{d^2x}{dt^2}\)
2. Uniform Acceleration
The differential equation of motion for a particle of constant of uniform acceleration in a straight line is simple:
The acceleration is constant.
So the second derivative of the position of the particle is constant.
3. Constant translational acceleration in a straight line
These equations apply to a particle, moving linearly, in 3 dimensions in a straight line with constant acceleration. Since the position, velocity, and acceleration are colinear (parallel, lie on the same line), only the magnitudes of these vectors are necessary, and because the motion is along straight line, the problem effectively reduces from 3 dimensions to 1 dimension.
Using acceleration definition \(a = \frac{dv}{dt} \to dv = a dt \to \int_{v=v_i}^v{dv} = \int_{t=t_i}^t{a dt} \to\)
[Eq. 1] \(v = v_i + at\)
Using [Eq. 1] \(v = \frac{dx}{dt} \to dx = vdt \to dx = (v_i + at)dt \to \int_{x=x_i}^x{dx} = \int_{t=t_i}^t{(v_i+at)}dt\)
[Eq. 2] \(x = x_i + v_it + \frac{1}2at^2\)
From [Eq. 1] we know \(v = v_i + at \to a = \frac{v-v_i}t\)
When we apply this to [Eq. 2] \(x = x_i + v_it + \frac{1}2at^2 \to x = x_i + v_it + \frac{1}2\frac{v-v_i}tt^2\)
[Eq. 3] \(x = x_i + \frac{1}2(v+v_i)t\)
We know \(a = \frac{dv}{dt} \land v = \frac{dx}{dt} \to dt = \frac{dv}{a} = \frac{dx}{v} \to \int_{x=x_i}^x{adx} = \int_{v=v_i}^v{vdv} \to a(x - x_i) = \frac{(v^2-v_i^2)}{2} \to\)
[Eq. 4] \(v^2=v_i^2+2a(x-x_i)\)
These four equations are quite handy for calculations of trapezoidal speed profiles.